这是一道简单的计算几何问题。

$\text{Simson theorem}$

定理： 过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线上的垂线，则三垂足共线，此线称为 $\text{Simson line}$。

逆定理： 若一点在三角形三边所在直线上的射影共线，则该点在此三角形的外接圆上。

这里借用官方题解的一张图。

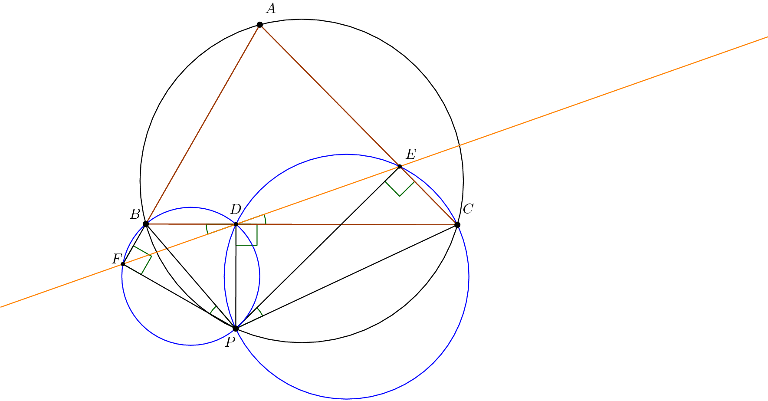
如图，$\triangle ABC$ 的外接圆上有一点 $P$，作 $PD\perp BC,PE\perp AC,PF\perp AB$，则 $E,D,F$ 三点共线。

证明：

$\because \angle AFP=\angle AEP=90^\circ$

$\therefore \angle A+\angle EPF=180^\circ$

$\because \angle ABP=\angle ACP=90^\circ$

$\therefore \angle A+\angle BPC=180^\circ$

$\therefore \angle BPC=\angle EPF$

$\therefore \angle BPF= \angle CPE$

$\because \angle BPF=\angle BDF,\angle CPE=\angle CDE$

$\therefore \angle BDF= \angle CDE$

$\therefore E,D,F\text{三点共线}$

$\mathtt{Q.E.D.}$

有了这个定理，我们就可以在 $\mathrm{O(n^2)}$ 或 $\mathrm{O(n^2log_2n)}$ 内解出这道题啦。

首先，枚举垂足，然后算出它与其他未统计的垂足的斜率，统计答案，单独考虑重合的点。

设不同斜率的点数为 $a_1,a_2,a_3,\cdots,a_k$，则答案为 $C_{a_1}^2+C_{a_2}^2+\cdots+C_{a_k}^2$（$C$ 表示组合数）。对于重合的点，可以选择两个重合点再选择另一个点，三点一定共线。

代码

#include<cstdio>
#include<algorithm>
#define eps 1e-12
double x[2010],y[2010],p[2010];
double abs(double x){
	return x>0?x:-x;
}
long long n,ans;
int main(){
	scanf("%lld",&n);
	for(int i=1;i<=n;i++){
		double a,b,c;
		scanf("%lf%lf%lf",&a,&b,&c);
		c=-c;
		x[i]=-a*c/(a*a+b*b);
		y[i]=-b*c/(a*a+b*b); 
	}
	for(int i=1;i<=n-2;i++){
		int k=0,kk=0,dd=1;
		for(int j=i+1;j<=n;j++)
			if(abs(x[i]-x[j])<=eps&&abs(y[i]-y[j])<=eps)++kk;
			else if(abs(x[i]-x[j])>=eps)
				p[++k]=(y[i]-y[j])/(x[i]-x[j]);
			else p[++k]=1e20;
		for(int j=1;j<=kk;j++)ans+=n-i-j;
		std::sort(p+1,p+k+1);
		for(int j=1;j<=k;j++){
			while(abs(p[dd]-p[j])>eps)dd++;
			ans+=j-dd;
		}
	}
	printf("%lld",ans);
	return 0;
}