第一眼想到圆方树，建出圆方树。

对于询问一，在圆方树上，原图的割边对应一个方点，如下图：

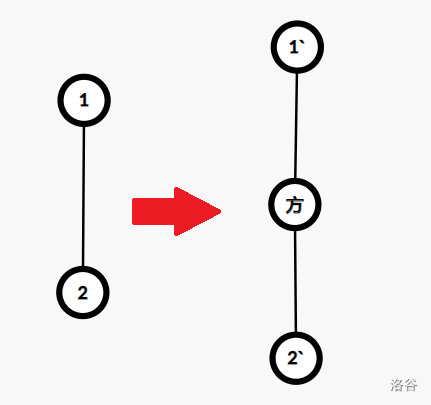
如果不是割边，答案一定为 yes，如果是割边，问题转化为问题二。

对于询问二，等价于询问在圆方树上 $A,B$ 两点间路径是否经过 $C$。

为什么正确？因为圆方树上的连通性等价于原图的连通性。

解决路径是否经过 $C$ 使用树剖可以方便解决，根本不用分类讨论：

int lca(int x,int y,int z){
	int p=0;
	while(top[x]!=top[y]){
		if(d[top[x]]<d[top[y]]){
			if(top[y]==top[z]&&d[z]<=d[y])p=1;
			y=f[top[y]];
		}else{
			if(top[x]==top[z]&&d[z]<=d[x])p=1;
			x=f[top[x]];
		}
	}
	if(d[x]>d[y])std::swap(x,y);
	if(top[x]==top[z]&&d[z]>=d[x]&&d[z]<=d[y])p=1;
	return p;
}

代码

#include<cstdio>
#include<algorithm>
#include<map>
#include<utility>
std::map<std::pair<int,int>,int> mp;
int ghead[100010],gto[1000010],gnxt[1000010],cnt;
int thead[200010],tto[400010],tnxt[400010],tcnt;
int n,m,*head(ghead),*to(gto),*nxt(gnxt),q;
void add(int const &x,int const &y){
	to[++cnt]=y,nxt[cnt]=head[x],head[x]=cnt;
}
void tadd(int const &x,int const &y){
	tto[++tcnt]=y,tnxt[tcnt]=thead[x],thead[x]=tcnt;
}
int s[100010],tp,ncnt,low[100010],dfn[100010];
void tarjan(int const &x,int const &fa){
	low[x]=dfn[x]=++cnt;
	s[++tp]=x;
	for(int i=head[x];i;i=nxt[i])
		if(!dfn[to[i]]){
			tarjan(to[i],x);
			low[x]=std::min(low[x],low[to[i]]);
			if(low[to[i]]>=dfn[x]){
				++ncnt;
				if(low[to[i]]>dfn[x])mp[std::minmax(x,to[i])]=ncnt;
				do{
					tadd(s[tp],ncnt),tadd(ncnt,s[tp]);
				}while(s[tp--]!=to[i]);
				tadd(x,ncnt),tadd(ncnt,x);
			}
		}else if(to[i]!=fa) low[x]=std::min(low[x],dfn[to[i]]);
}
int d[200010],f[200010],sz[200010],son[200010],top[200010];
void dfs1(int const &x,int const &fa){
	d[x]=d[fa]+1,f[x]=fa,sz[x]=1;
	for(int i=head[x];i;i=nxt[i])
		if(to[i]!=fa){
			dfs1(to[i],x);
			sz[x]+=sz[to[i]];
			if(sz[to[i]]>sz[son[x]])son[x]=to[i];
		}
}
void dfs2(int const &x,int const &tp){
	top[x]=tp;
	if(son[x]) dfs2(son[x],tp);
	for(int i=head[x];i;i=nxt[i])
		if(to[i]!=f[x]&&to[i]!=son[x])
			dfs2(to[i],to[i]);
}
int lca(int x,int y,int z){
	int p=0;
	while(top[x]!=top[y]){
		if(d[top[x]]<d[top[y]]){
			if(top[y]==top[z]&&d[z]<=d[y])p=1;
			y=f[top[y]];
		}else{
			if(top[x]==top[z]&&d[z]<=d[x])p=1;
			x=f[top[x]];
		}
	}
	if(d[x]>d[y])std::swap(x,y);
	if(top[x]==top[z]&&d[z]>=d[x]&&d[z]<=d[y])p=1;
	return p;
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1,x,y;i<=m;i++)scanf("%d%d",&x,&y),add(x,y),add(y,x);
	ncnt=n,cnt=0;
	tarjan(1,0);
	head=thead,nxt=tnxt,to=tto;
	dfs1(1,0),dfs2(1,1);
	scanf("%d",&q);
	while(q--){
		static int op,a,b,c,d;
		scanf("%d",&op);
		if(op==1){
			scanf("%d%d%d%d",&a,&b,&c,&d);
			std::map<std::pair<int,int>,int>::iterator it=mp.find(std::minmax(c,d));
			if(it==mp.end())puts("yes");
			else puts(lca(a,b,it->second)?"no":"yes");
		}else{
			scanf("%d%d%d",&a,&b,&c);
			puts(lca(a,b,c)?"no":"yes");
		}
	}
	return 0;
}