如果这篇博客帮助到你，可以请我喝一杯咖啡~
CC BY-NC-SA 4.0 （除特别声明或转载文章外）
Ynoi 做题记录
Latest Updated on: 2023.12.14
[Ynoi2001] 雪に咲く花
题意
给定三个长为 $n$ 序列 $a,b,c$，每次询问一个区间 $[l,r]$，求 $(a_l\operatorname{bitand} \cdots\operatorname{bitand} a_r)\times(b_l\operatorname{bitor} \cdots\operatorname{bitor} b_r)\times\gcd(c_l,\cdots,c_r)$。
不强制在线
题解
首先考虑离线扫描线，扫描 $r$，然后对每个 $i$ 维护 $l\le i$ 的答案之和 $s_i$，这样答案就可以写为 $s_r-s_{l-1}$。
我们设 $A_i=a_i\operatorname{bitand} \cdots\operatorname{bitand} a_r$，$B_i=b_i\operatorname{bitor} \cdots\operatorname{bitor} b_r$，$C_i=\gcd(c_i,\cdots,c_r)$。
然后考虑 $r$ 向右移 $1$，这个时候 $s_i$ 的变化量，如果 $A_i,B_i,C_i$ 都没有发生变化，那么 $s_i$ 的变化量也和上次右移的时候一致，所以我们可以把每个 $s_i$ 写成 $p_ir+q_i$ 的形式，那么需要修改 $p_i,q_i$ 的 $i$ 就只有 $A_i,B_i,C_i$ 发生变化的部分，由于 $A_i,B_i,C_i$ 都只会发生 $O(\log v)$ 次修改（$v$ 是值域），所以总变化次数只有 $O(n\log v)$ 次，暴力修改即可。
[Ynoi2002] Goedel Machine
题意
给定一个长为 $n$ 的数列 $a$，每次询问一个区间 $[l,r]$，求区间内所有非空子序列的最大公约数的乘积，对 $998244353$ 取模，值域与 $n$ 同阶。
不强制在线
题解
考虑对每一个质数及其幂分开计算。
考虑所有小于根号的质数，及其质数幂，这样的数总共有 $O(\sqrt n)$ 个，枚举每一个，扫一遍序列预处理，查询可以 $O(1)$。
剩余部分为所有大于根号的质数，每个数只有一个这样的因子，莫队解决。
[Ynoi2003] 博丽灵梦
题意
给定平面上 $n$ 个点，多次查询矩形区域所有点的颜色的权值之和，两个点颜色相同只统计一次。
不强制在线
题解
对第一维莫队，问题改为序列问题， $O(1)$ 插入删除 $O(\sqrt n)$ 求区间颜色权值和。
根据经典套路，转化为 $(i,pre_i)$ 的二维数点，问题即为 $O(1)$ 插入一个点，$O(\sqrt n)$ 查询一个位置的二维前缀和，与 [Ynoi2007] rdiq 的分块方式一致只是从 $O(\sqrt n)-O(1)$，变成 $O(1)-O(\sqrt n)$，没有区别，不多赘述。
对于莫队时动态维护 $pre_i$ 我们可以使用只删不加的回滚莫队配合链表完成。
时间复杂度 $O(n\sqrt m+m\sqrt n)$。
[Ynoi2003] 雾雨魔理沙
题意
懒得描述了，放个原题面，大概就是你要维护树上邻域信息，$O(n\log n)$ 预处理，$1$ 次合并查询。
强制在线
题解
建出全局平衡二叉树，维护出簇内距离界点各个距离时的信息，再类似于换根 dp 的方式维护出每个簇外距离界点各个距离时的信息（只需要维护簇直径大小的信息）。查询时，定位到最大的被邻域完全覆盖的簇，然后可以将邻域划分为一个界点外的信息+簇信息+另一个界点外的信息，两次合并，预处理的时候把簇信息塞到另外两个其中一个里面就是一次合并。
[Ynoi2005] rpxleqxq
题意
给定一个长为 $n$ 的数列 $a$，每次询问一个区间 $[l,r]$，问有多少个二元组满足 $l\le i<j\le r\land(a_i\oplus a_j)\le x$，值域与 $n$ 同阶。
不强制在线
题解
莫队二离，问题转化为维护一个集合，$O(\sqrt n)$ 插入一个数，$O(1)$ 查询这个数和多少个集合内的数异或起来 $\le x$。
我们知道 $x\oplus a\le b$ 的解集是 $\log$ 个形如 $[a2^i,(a+1)2^i)$ 的区间，我们对值域根号分治，这样 $2^i\le 2^p$ 的部分区间长度不会超过 $2^p$，$2^i>2^p$ 的部分，我们记录 $\frac {a2^i}{2^p}$，区间长度也不会超过 $2^p$。
[Ynoi2005] qwq
题意
给定一个正整数序列 $a$ 和一个数 $m$，多次询问一个区间，进行至少多少次操作后区间会变为全 $0$，一次操作定义为给一个长度不超过 $m$ 的区间减一。
不强制在线
题解
考虑给定一个序列，怎么求答案，我们发现每次对一个最长的不超过 $m$ 的递增序列进行操作，这样的操作数即为答案。
我们称一个 $a_i>a_{i+1}$ 为一个 gap，考虑预先消去这些 gap，即对于一个 gap，提前给 $a_{i-m+1\sim i}$ 减去 $a_i-a_{i+1}$，然后求解的变成每次对一个长为 $m$ 的序列减 $1$，至少多少次每个数都变成非正数，再加上预先消去 gap 的次数（即 $\sum\max(0,a_i-a_{i+1})$）。
正确性证明：对于一个递增序列，显然这么做的答案是一样的。
我们发现每次对一个长为 $m$ 的序列减 $1$，至少多少次每个数都变成非正数，这个问题等价于选出若干个数，两两距离至少为 $m$，最大化选出的数的和。
在转化问题的时候还有一个问题，由于原问题是区间查询，所以可能存在最后 $m$ 个位置被区间外的 gap 干扰的情况，我们发现最后 $m $ 个数消去 gap 后的操作次数一定是 $a_r$（因为是递增序列），所以我们可以转化为 $[l,r)$ 的 gap 消去次数加 $a_r$ 加 $[l,r-m]$ 中选出若干个数，两两距离至少为 $m$，最大化选出的数的和。
现在问题就是怎么求一个区间选出若干个数，两两距离至少为 $m$，最大化选出的数的和。
- 若 $m\le \sqrt n$
- 考虑找到 $k=\frac n2$，对于跨过 $k$ 的询问，我们进行处理，对于不跨过 $k$ 的询问，我们把问题转化为问题规模为 $(\frac n2,m)$ 的子问题。
- 对于对于跨过 $k$ 的询问，一定存在一个跨过 $k$ 的 $m-1$ 的全不选的区间，枚举这个区间，对于一个区间 $[l,r]$，考虑利用 dp 求出 $\forall i<l,i\sim l-1$ 和 $\forall i>r,r+1\sim i$ 的答案，然后对于询问 $L,R$，用 $dp_L+dp_R$ 更新答案，预处理时间复杂度 $O(nm)=O(n\sqrt n)$，对于单个询问，时间复杂度 $O(m)=O(\sqrt n)$。
- 若 $m> \sqrt n$
- 考虑把序列按顺序写成若干行，一行 $m$ 个数，再次分类讨论。
- 若询问区间中存在一行为空
- 枚举为空的一行，两侧的选择互不干扰，和上面一样处理出 $\forall i<l,i\sim l-1$ 和 $\forall i>r,r+1\sim i$ 的答案，预处理时间复杂度 $O(n\frac nm)=O(n\sqrt n)$，对于单个询问，时间复杂度 $O(\frac nm)=O(\sqrt n)$。
- 若询问区间每一行均不为空
- 我们考虑设 $k=\lfloor\frac n2\rfloor$，把一行分为前 $k$ 个和后 $m-k$ 个。
- 由于每一行均不为空，下一行选择的位置一定在当前行选定位置的右下方，如果第一行选定位置在前 $k$ 个中，最后一行选定位置在后 $m-k$ 个中，那么，我们将每一行的后 $m-k$ 个与下一行的前 $k$ 个拼接起来，一定存在一个新行为空，跑上面的算法即可。
- 现在第一行选定位置和最后一行选定位置一定在 $k$ 的同一侧了。
- 我们发现，如果第一行选定位置和 $l$ 不在同一侧或最后一行选定位置和 $r$ 不在同一侧，那么这样的答案一定在上面的计算中可以求出。
- 所以只有 $l$ 和 $r$ 在同一侧的询问会需要继续求解，发现此时问题规模变成 $(\frac n2,\frac m2)$。
对于预处理时间复杂度为 $T(n)=2T(\frac n2)+O(n\sqrt n)=O(n\sqrt n)$，对于单个询问的时间复杂度 $T(n)=T(\frac n2)+O(\sqrt n)=O(\sqrt n)$。
[Ynoi2005] tdnmo
题意
不太好描述，放个原题面，大概就是树上有向邻域莫队的意思。
题解
树分块，分块大小 $\frac{n}{\sqrt m}$，对于询问分类讨论
- 如果邻域完全在同一块内，点数不会超过 $\frac{n}{\sqrt m}$，暴力加入然后撤回；
- 否则，询问点一定在界点间的路径上，对于同一块的询问，按照 $dep_x+y$ 排序，实际上就是回滚莫队，设这个块下方的界点为 $u$，先达到 $N(u,dep_x+y-dep_u)$，再达到 $N(x,y)$，再撤回就好了。
[Ynoi2005] vti
题意
给定一棵有根树，边有边权，每次询问给定一个点集，设 $S$ 为点集内两两路径经过的所有边的集合，问从 $S$ 中可以找到多少对 $(i,j)$ 使得 $i$ 是 $j$ 的祖先且 $a_i<a_j$，两条边 $a,b$，$a$ 是 $b$ 的祖先当且仅当 $a$ 连接的深度较深的点是 $b$ 连接的深度较深的点的祖先。
题解
我们考虑把这个问题转化为树上链查询，建出询问点集的虚树 $T$，设虚树根为 $rt$，答案即为 $\sum\limits_{u\in leaf(T)}f(rt,u)-\sum\limits_{u\in T\land u\notin leaf(T)}(s_u-1) f(rt,u)$，其中 $leaf(T)$ 表示虚树的所有叶子，$s_u$ 表示 $u$ 的儿子数，$f(a,b)$ 表示 $a$ 到 $b$ 这条链的答案，这样拆分后总询问数不会超过 $\sum (2t_i-1)$，且每个询问内两点都是祖先关系。
莫队二离，把树分块 $O(\frac{n}{\sqrt m})$，直接在树上跑莫队就好。
[Ynoi2006] rldcot
题意
给定一棵有根树，边有边权，每次询问给定 $l,r$，求 $\mid\begin{Bmatrix}\operatorname{dep(\operatorname{lca}(i,j))}\mid l\le i,j\le r\end{Bmatrix}\mid$。
不强制在线
题解
我们把询问离线，按右端点排序，维护每一个左端点的虚树的答案。
我们新加入一个点 $i$，虚树上最多加两个点，其中一个是这个点本身，影响到了左端点为 $[1,i]$ 的虚树。
另一个点我们在 $\text {LCT}$ 上 $\text{access}$ 一下，将这个点到根的链的权值赋值为 $i$。
$\text{access}$ 时经过的每一条虚边的父亲就是可能的一个新增的节点，其影响到的虚树是一个前缀（其实是一个区间，但前面的每颗虚树都已经有这个点了，我们再加一遍也没事），前缀大小就是这个节点的权值。
那么现在问题变为，我们有 $n$ 个集合，$O(n\log n)$ 次修改，一次修改形如向一个前缀中加入一个颜色，一次查询形如单点查询集合大小。
我们对每种颜色记录当前长度为多少的前缀已经包含这种颜色，称为 $pos_i$，那么一次修改就是区间 $(pos_i,k]$ 加 $1$，$pos_i\larr \max(pos_i,k)$，一次查询就是单点查询，树状数组解决。
时间复杂度 $O(n\log^2n+m\log n)$，空间复杂度 $O(n+m)$。
[Ynoi2006] rmpq
题意
给定含幺半群 $(D,,e)$，平面上每个点有点权 $d(x,y)$，初始时为单位元 $e$，每次修改给定一条平行于 $x$ 轴或 $y$ 轴的直线，把平面分成两部分，再给定 $d1,d2\in D$，对于上/左部分内的所有点，$d(x,y)\larr d(x,y)d1$，对于另一部分内的所有点 $d(x,y)\larr d(x,y)*d2$。
要求你支持查询一个点的点权 $d(x,y)$，限制总 $*$ 运算使用次数。
强制在线
题解
因为不具有交换律，所以信息必须按照时间维护，我们考虑所有修改在询问前的做法，把修改按照 $O(B)$ 分块，对于每一块，我们进行一个 $O(B^2)$ 的算法，求出 $O(B^2)$ 个区域分别的修改，就直接分治就行了 $T(B)=2T(\frac B2)+O(B^2)=O(B^2)$，对于查询时，在每个块中查出对应的修改，乘起来就好了。
现在考虑动态怎么做，我们考虑二进制分组，在组大小到达 $B$ 后就不继续合并了，构建一组的复杂度就是 $F(B)=2F(\frac B2)+T(B)=O(B^2)$。
[Ynoi2006] spxmcq
题意
给一棵有根树，点有点权，询问给定节点 $u$ 和参数 $x$，求：假如所有点权加 $x$ ，完全在 $u$ 子树内的包含 $u$ 的联通点集的权值之和最大值。
不强制在线
题解
$f_u=a_u+x+\sum\max(0,f_v)$，$v$ 是 $u$ 的儿子，显然在 $x$ 增大的过程中，$f_u$ 不降，所以 $\max(0,f_v)$ 的决策只会发生一次从 $0$ 到 $f_v$ 的改变，并且每个点的 $f$ 都可以表示成 $ax+b$ 的一次函数，把询问离线下来，按照 $x$ 排序，然后再用堆维护决策的改变，按照 $x$ 从小到大处理询问，把当前所有改变的决策都处理一遍，用并查集维护所有决策是 $f_v$ 的边形成的连通块，决策改变就是链加，查询单点权值就是单点查询。
[Ynoi2006] wcirq
题意
你需要维护一个序列，支持插入，用若干个集合定位一个区间。$n\le 10^6$
即你有 $2\times10^7$ 个集合，你可以向其中某个加入一个元素，每次插入限定使用 $64$ 次。
你可以选取最多 $256$ 个集合，两两无交，以它们的并集为答案回答一个询问。
强制在线
题解
我们想到用平衡树维护这个东西，但常见的平衡树都是均摊和期望的，所以我们考虑固定每一层的集合大小和深度，便于分析复杂度。
我们构造一个 Leafy Tree，第 $i$ 层的节点对应的集合大小为 $[4^{i-1},4^i)$，叶子（第 $0$ 层）节点大小为 $1$。
单次插入的操作次数就是深度，也就是 $11$ 的样子。
一个节点最多有 $15$ 个儿子，所以查询的操作次数大概在深度乘二倍的儿子数左右，常数很小，应该能控制在 $256$ 次内。
现在的问题就是插入后如果一个节点集合大小超过了上界，如何处理。
考虑分裂，但是分裂后的集合需要重新维护，我们如果暴力插入的话，均摊复杂度显然是正确的，但我们要保证 Worst Case，所以不能暴力。
我们认为一个集合大小等于 $3\times 4^{i-1}$ 的节点是即将分裂的，这样的节点再进行 $4^{i-1}$ 次插入就会分裂，我们维护它分裂出的两个集合，每进行一次插入就向分裂后的集合进行四次插入，这样当它分裂时，我们正好维护出了它分裂出的两个集合，这里有一点小细节，就是我们要保证分裂出的集合大小在 $[4^{i-1},4^i)$，并且要恰好把儿子分成两部分。
[Ynoi2007] rfplca
题意
给定一棵树，以 $fa$ 序列给出，保证 $fa_i<i$，支持两种操作：
- 对于所有 $l\le i\le r$，$fa_i\larr \max(fa_i-x,1)$；
- 查询 $u,v$ 两点 $\operatorname{LCA}$。
强制在线
题解
序列分块，处理出每个点跳出本块的第一个祖先 $b_i$，对于零散修改直接暴力，对于一个块，前 $\sqrt{n}$ 次整块修改直接暴力修改，这之后块内每一个数都满足 $fa_i=b_i$，打标记即可，查询直接做就行了。
[Ynoi2007] rdiq
题意
给定一个序列，求区间本质不同逆序对数量。
不强制在线
题解
莫队二离，右端点移动的贡献即为 $[l,r]$ 中 $>a_r$ 的权值种数减去 $[l,pre_r]$ 中 $>a_r$ 的权值种数。
容易发现我们需要一个支持 $O(\sqrt n)$ 单点加 —— $O(1)$ 查询矩形和的数据结构。
如图，我们将一个询问划分成若干部分：
- 红色部分：大小为 $n^{0.75}\times n^{0.75}$，一个询问最多包含完整的 $n^{0.25}\times n^{0.25}$ 个块。
- 蓝色部分：大小为 $n^{0.75}\times n^{0.5}$，剩余区域中最多包含的 $n^{0.25}\times n^{0.25}$ 个块。
- 紫色部分：大小为 $n^{0.5}\times n^{0.75}$，剩余区域中最多包含的 $n^{0.25}\times n^{0.25}$ 个块。
- 绿色部分：大小为 $n^{0.5}\times n^{0.5}$，剩余区域中最多包含的 $n^{0.25}\times n^{0.25}$ 个块。
- 棕色部分：散块。
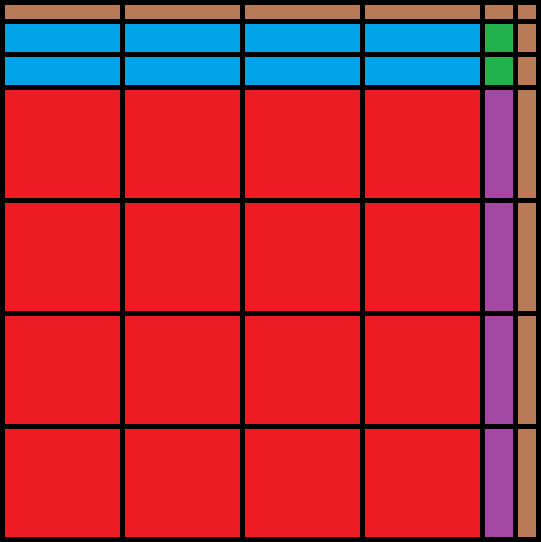
对上述除散块部分维护前缀和，对于散块，询问只有 $n$ 种，横坐标和纵坐标两两不同，而散块宽度只有 $O(\sqrt n)$ 种，涉及到的询问只有 $O(\sqrt n)$ 种，遍历一遍即可。
[Ynoi2007] rvrewsus
题意
给定一个长为 $n$ 的序列 $a$ 和一个数 $b$，每次查询给出两个区间 $[l,r],[L,R]$，设序列 $a$ 在区间 $[l,r]$ 内值在 $[L,R]$ 之间的数组成的集合（不可重）为 $S$。
求 $\sum\limits_{k=1}^{\mid S\mid}\operatorname{min}_{k}(S)b^k$，其中 $\operatorname{min}_k(S)$ 表示 $S$ 中第 $k$ 小的数，答案对 $333333333333333397$ 取模。
不强制在线
题解
哈希值这一信息，如果值域不交，是可以简单合并的。
如果值域只有边界上的一个数有交，也是可以简单合并的。
所以如果一个值存在多个位置，我们也把它当成多个值来处理，不把相同的值合到一起。
然后对值域做 [Ynoi2013] D2T2 的分块分治就完事了。
[Ynoi2007] TB5x
题意
不太好描述，放个原题面。
题解
考虑这样一个问题，给出平面上 $n$ 个点，$m$ 条线，每条线把平面分成两部分，我们可以判定一个点在线的哪一侧，然后我们要按顺序对每根线的某一侧进行修改查询，操作离线，也就是说，我们要建立一种数据结构可以定位每根线的某一侧。
我们称 $f(m)$ 为 $m$ 条线把平面分成多少部分，那么，每个部分形成一个等价类，即进行相同的修改，我们对每个等价类建立一个节点，儿子是等价类内的所有点，维护的信息即合并子节点信息。
考虑减小问题规模，我们进行分治，把线按照操作时间分为两部分，先处理较早的操作，这部分只有 $f(\frac m2)$ 个等价类，每个等价类都是上一层若干个的并，那么我们对每个新等价类建立一个节点，儿子是这些上一层的等价类，维护的信息即子节点信息的合并。
我们分治到 $m=1$ 的时候，这样就得到了我们要进行修改或查询的等价类，修改直接打 tag，回溯到上一层时下放标记，这样做的复杂度为 $T(m)=2T(\frac m2)+O(\min(f(m),n))$。
对于这道题，由于为直线 $f(m)=m^2$，所以 $T(m)=2T(\frac m2)+O(\min(m^2,n))$。
这里似乎直接分治所有询问复杂度就是对的？但好像不好写的样子。我们考虑一种实现方式，把询问按照 $B=\sqrt n$ 分组，每一组进行一次分治，这样复杂度就是 $O(m\sqrt n)$，也更好实现。
对于这道题，还有一个实现上的难点，就是交换操作导致我们无法分治时自上而下构建出这个数据结构。我们从分治的叶子节点开始构造这个数据结构，也就是从这个数据结构的根开始构建，注意到两维对称，这里只讲解一维时的情况。
进行完叶子节点的交换操作后的一维是一个由三个连续段构成的排列，一个节点的排列就是两个子节点的复合，段数为 $a$ 和 $b$ 的复合最多 $a+b$ 段，所以复杂度是对的，然后一个段就是一个等价类，这里左儿子的段向父亲的段的连边是值对应相连，右儿子的段向父亲的段的连边是位置对应相连。
这样我们就建立出了这个数据结构，这道题就做完了，时间复杂度 $O(n+m\sqrt n)$。
[Ynoi2008] rupq
题意
给定一个序列，每个位置有一个括号和一个 $32$ 位无符号整形，要求支持单点修改，查询区间未匹配括号处的最大值和按位与非的结果，交换两个区间。
不强制在线
题解
与非是没有结合律的，考虑用 [Ynoi2017] 由乃的 OJ 的方法维护。
先考虑如何使用线段树维护前两个操作，第三个操作就是换成平衡树。
一个区间的未匹配括号形如 $\text{)(}$，我们考虑分成两部分维护，$\text{)}$ 和 $\text{(}$，这样在合并两个区间时得到的结果分为三部分，左区间的左半部分，左区间的右半部分和右区间的左半部分消掉后的部分，右区间的右半部分。
我们每个点存一下左区间的右半部分和右区间的左半部分消掉后的部分，求这个东西时我们可以在这个点的子树内查询一下就行了。
[Ynoi2008] rplexq
题意
给定一棵有根树，每次询问 $l,r,x$，查询 $\sum\limits_{i=l}^r\sum\limits_{j=l+1}^r[\operatorname{lca}(i,j)=x]$。
不强制在线
题解
考虑对 $x$ 的儿子数根号分治。
小于等于 $\sqrt n$，对于这样的节点，使用分块进行二维数点，求出每个子树在区间 $l,r$ 内的节点数量 ，复杂度为 $O((n+m)\sqrt n)$。
大于 $\sqrt n$，对于这样的节点，我们枚举儿子 $v$，遍历这棵子树，将所有节点标记上 $v$，发现 $x$ 子树内不合法的方案数类似于小 Z 的袜子，可以用莫队维护，复杂度为 $O(\sum n_i\sqrt m_i)$。其中 $\sum m_i=O(m)$，$n_i=O(n),\sum n_i=O(n\sqrt n)$，复杂度显然不对，我们希望一个点只出现在一次莫队中，这样 $\sum n_i=O(n)$，总复杂度即为 $O(n\sqrt m)$。
考虑按 dfs 序倒序处理，保证 $x$ 处理时子树内儿子数量大于 $\sqrt n$ 的节点已被处理。
我们将 $x$ 的子树分为两类，一类是没有节点被访问过的，一类是存在节点被访问过的。
对于未被访问的节点，跑离散化莫队；对于访问过的节点，显然包括这种节点的子树不超过 $O(\sqrt n)$ 个，使用分块对这些子树分别维护一下即可。
最后再进行一次 $O((n+m)\log n)$ 的二维数点得到总情况数减掉算出来的非法方案数就是答案了。
[Ynoi2008] rrusq
题意
给定 $n$ 个关键点，$m$ 个矩形，在同一个二维平面上，每个关键点有权值，每次查询一个区间 $l,r$，求矩形 $l\sim r$ 的并覆盖到的关键点权值和。
不强制在线
题解
一个常用套路，把询问离线下来，按照 HH 的项链的做法，向右挪动右端点，用一种数据结构维护左端点在不同位置的答案。对于一个关键点，我们只在最靠右的覆盖它的矩形处统计，使用 $\rm{KDT}$ 维护点，对于每个矩形打上标记，遇到已经打上标记的点，将标记收回，这里的复杂度显然是 $O(m\sqrt n)$ ，也就是说，我们维护答案的数据结构会收到 $O(m\sqrt n)$ 次修改，$O(q)$ 次询问，使用分块维护。
[Ynoi2008] stcm
题意
支持向集合内加入一个点，撤销上一次加入操作，标记当前集合为 $i$ 的子树补信息，求构造一个操作序列使得所有点的子树补信息都被正确标记。
节点 $i$ 的子树补信息定义为不在 $i$ 子树内的所有点。
题解
假设重链链首的子树补信息已被正确标记，我们可以得到所有这条重链上的点的子树补信息，这部分总复杂度 $O(n\log n)$。
对一条重链的所有轻儿子建立哈夫曼树，每个轻儿子的权值为其子树的大小，进入左子树时加入右子树所有点，进入右子树时加入左儿子所有点，每跳过一个轻链大小翻倍，每在哈夫曼树上跳两次父亲大小翻倍，这部分总复杂度 $O(n\log n)$。
[Ynoi2008] rsmemq
题意
给定一个序列，每次询问一个区间 $l,r$，求有多少区间 $l’,r’$ 满足 $l\le l’\le r’\le r$，且区间长度为奇数且 $\frac{l’+r’}2$ 是区间的众数。
不强制在线
题解
枚举中心 $i$，存在若干段半径 $[l,r]$ 满足条件，这样的总段数不超过 $n$，因为一段对应一个数的一种出现次数，求出这 $n$ 段后，问题变为有若干条平行于 $y$ 轴的线段，每次询问一个由两条斜率分别为 $1,-1$ 的线段和 $x$ 轴围成的区域内的线段长度和，树状数组即可，时间复杂度 $O((n+m)\log n)$。
考虑如何求出这 $n$ 段，我们有个想法，对于每一段，二分+区间众数，复杂度 $O(n\sqrt n\log n)$，显然是过不去的。
考虑根号分治，对于出现次数大于根号的，暴力扫一遍序列即可；对于出现次数小于根号的，对于每种出现次数 $k$，我们 $O(n)$ 求出最小的 $p_i$ 满足 $[i,p_i]$ 恰好众数出现次数为 $k$，对于出现次数为 $k$ 的端我们二分出它的端点即可，时间复杂度 $O(n\sqrt n+n\log n)$。
[Ynoi2008] rdCcot
题意
给定一棵树，和一个常数 $C$，把每个点和与其距离小于等于 $C$ 的点连边形成一张新图，多次查询只保留编号在 $[l,r]$ 内点的连通块个数。
不强制在线
题解
我们有个 naive 的想法，预处理出和每个节点编号最接近的距离在 $C$ 以内的两个（一个大于 $x$，一个小于 $x$）节点，然后莫队并查集，于是你写了，过样例了，交了，WA 了。
冷静思考一下可以发现这种做法是显然错误的，我们注意到我们 $2n$ 个信息中有重复的，有用的信息没有记录下来，为了获取尽可能多的信息，我们对于编号为 $x$ 的点，记录编号最接近的两个距离在 $C$ 以内且满足 $dep_i<dep_x\lor(dep_i=dep_x\land i<x)$ 的点，记为 $l_i,r_i$。
我们可以把询问从数连通块变为数 $l_i<l\land r_i>r$ 的点数量，为什么这么做是正确的？
因为 $dep_i<dep_x$，所以每个连通块只有深度最浅的一层点可以满足 $l_i<l\land r_i>r$ 的性质；因为 $dep_i=dep_x\land i$，同层点只有一个满足 $l_i<l\land r_i>r$ 的性质。
我们注意数据范围，猜想正解复杂度为 $O(n\log^2 n+m\log n)$。
首先，预处理出上面说的这个东西可以用点分治，对于每一个分治中心，我们把点按 $dep$ 排序插入平衡树内，平衡树节点维护到分治中心的 $dis$ 最小值，查询时直接平衡树上二分就可以了。
问题转化为每个点有两个属性 $l_i,r_i$，当 $l_i<l\land r_i>r$ 时，$i$ 对询问区间 $[l,r]$ 产生 $1$ 的贡献，直接把询问离线下来用树状数组维护答案就可以了，不会的可以去做 HH 的项链。
[Ynoi2009] rprsvq
题意
给定一个长为 $n$ 的序列，支持两种操作：
- 区间加；
- 区间中所有子序列的方差和。
不强制在线
题解
一个序列的方差为：
\[\begin{aligned} &\frac{1}{n}\sum\limits_{i=1}^{n}(a_i-\overline{a})^2\\ =&\frac{1}{n}\sum\limits_{i=1}^{n}(a_i^2-2a_i\overline{a}+\overline{a}^2)\\ =&\frac{1}{n}\sum\limits_{i=1}^{n}a_i^2-\frac{2\overline{a}}{n}\sum\limits_{i=1}^{n}a_i+\overline{a}^2\\ =&\frac{1}{n}\sum\limits_{i=1}^{n}a_i^2-\overline{a}^2\\ =&\frac{1}{n}\sum\limits_{i=1}^{n}a_i^2-\frac{1}{n^2}(\sum\limits_{i=1}^na_i)^2\\ =&\frac{n-1}{n^2}\sum\limits_{i=1}^{n}a_i^2-\frac{2}{n^2}\sum\limits_{i=1}^n\sum\limits_{j=i+1}^na_ia_j\\ \end{aligned}\]那么，对于一个区间的答案就是：
\[\begin{aligned} &\sum\limits_{n=2}^{r-l+1}(\frac{n-1}{n^2}\binom{r-l}{n-1}\sum\limits_{i=l}^{r}a_i^2-\frac{2}{n^2}\binom{r-l-1}{n-2}\sum\limits_{i=l}^r\sum\limits_{j=i+1}^ra_ia_j)\\ =&\sum\limits_{n=2}^{r-l+1}\frac{1}{n^2}(\binom{r-l-1}{n-2}(r-l)\sum\limits_{i=l}^{r}a_i^2-2\binom{r-l-1}{n-2}\sum\limits_{i=l}^r\sum\limits_{j=i+1}^ra_ia_j)\\ =&\sum\limits_{n=2}^{r-l+1}\frac{1}{n^2}\binom{r-l-1}{n-2}((r-l)\sum\limits_{i=l}^{r}a_i^2-2\sum\limits_{i=l}^r\sum\limits_{j=i+1}^ra_ia_j)\\ =&((r-l)\sum\limits_{i=l}^{r}a_i^2-2\sum\limits_{i=l}^r\sum\limits_{j=i+1}^ra_ia_j)\sum\limits_{n=2}^{r-l+1}\frac{1}{n^2}\binom{r-l-1}{n-2}\\ =&((r-l+1)\sum\limits_{i=l}^{r}a_i^2-(\sum\limits_{i=l}^ra_i)^2)\sum\limits_{n=2}^{r-l+1}\frac{1}{n^2}\binom{r-l-1}{n-2}\\ \end{aligned}\]前面的东西可以用线段树维护，后面的东西继续推：
\[\begin{aligned} &\sum\limits_{n=2}^{x}\frac{\binom{x-2}{n-2}}{n^2}\\ =&\sum\limits_{n=2}^{x}\frac{\binom{x-2}{n-2}\binom{x}{2}}{n^2\binom{x}{2}}\\ =&\sum\limits_{n=2}^{x}\frac{\binom{x}{n}\binom{n}{2}}{n^2\binom{x}{2}}\\ =&\frac{1}{x(x-1)}\sum\limits_{n=2}^{x}\frac{\binom{x}{n}(n-1)}{n}\\ \end{aligned}\]设 $f_{x}=\sum\limits_{n=1}^{x}\frac{\binom{x}{n}(n-1)}{n}$。
\[\begin{aligned} f_x=&\sum\limits_{n=1}^{x}\frac{\binom{x}{n}(n-1)}{n}\\ =&\sum\limits_{n=1}^{x}\frac{(\binom{x-1}{n}+\binom{x-1}{n-1})(n-1)}{n}\\ =&\sum\limits_{n=1}^{x-1}\frac{\binom{x-1}{n}(n-1)}{n}+\sum\limits_{n=1}^{x}\frac{\binom{x-1}{n-1}(n-1)}{n}\\ =&f_{x-1}+\sum\limits_{n=1}^{x}\binom{x-1}{n-1}-\sum\limits_{n=1}^{x}\frac{\binom{x-1}{n-1}}{n}\\ =&f_{x-1}+2^{x-1}-\sum\limits_{n=0}^{x-1}\frac{\binom{x-1}{n}}{n+1}\\ =&f_{x-1}+2^{x-1}-\sum\limits_{n=0}^{x-1}\frac{\binom{x}{n+1}}{x}\\ =&f_{x-1}+2^{x-1}-\frac{2^x-1}{x}\\ \end{aligned}\]推到这里就可以 $O(n)$ 预处理系数了。
[Ynoi2009] rprmq1
题意
给定一个 $n\times n$ 的矩阵 $a$，初始全为 $0$，先进行 $m$ 次修改（矩形加），再进行 $q$ 次查询（矩形最大值）。
不强制在线
题解
将其中一维看作时间，则修改操作可以看做是 $l_1$ 时刻给区间 $l_2\sim r_2$ 加 $x$，$r_1+1$ 时间给区间 $l_2\sim r_2$ 减 $x$。查询操作即为 $l_1\sim r_1$ 时间内的区间最大值。我们用维护历史最值的线段树可以做到 $O(qm\log n)$ 。考虑对时间分治，先处理左区间，再处理右区间，然后处理跨越区间中线的询问。在处理一个区间前保证 $1\sim l-1$ 时间的操作均已加入线段树，然后加入 $l\sim mid$ 的操作，通过打标记的方式可以重置历史最值，现在把跨越中线的询问排序，分别处理左半部分和右半部分的贡献即可。
[Ynoi2009] rpdq
题意
给定一棵树，有边权，多组询问，求 $\sum\limits_{i=l}^r\sum\limits_{j=i+1}^r\operatorname{dis}(i,j)$。
不强制在线
题解
\[\begin{aligned} \sum\limits_{i=l}^r\sum\limits_{j=i+1}^r\operatorname{dis}(i,j)=&\sum\limits_{i=l}^r\sum\limits_{j=i+1}^r\operatorname{dep}(i)+\sum\limits_{i=l}^r\sum\limits_{j=i+1}^r\operatorname{dep}(j)-2\sum\limits_{i=l}^r\sum\limits_{j=i+1}^r\operatorname{dep}(\operatorname{lca}(i,j))\\ =&(r-l)\sum\limits_{i=l}^r\operatorname{dep}(i)-2\sum\limits_{i=l}^r\sum\limits_{j=i+1}^r\operatorname{dep}(\operatorname{lca}(i,j))\\ \end{aligned}\]前面的东西直接预处理前缀和 $O(1)$ 求就行，考虑维护后面的东西。
考虑莫队。
左端点从 $l+1$ 移动到 $l$ 的贡献为 $\sum\limits_{i=l+1}^r\operatorname{dep}(\operatorname{lca}(i,l))$；
左端点从 $l$ 移动到 $l+1$ 的贡献为 $-\sum\limits_{i=l+1}^r\operatorname{dep}(\operatorname{lca}(i,l))$；
右端点从 $r-1$ 移动到 $r$ 的贡献为 $\sum\limits_{i=l}^{r-1}\operatorname{dep}(\operatorname{lca}(i,r))$；
右端点从 $r$ 移动到 $r+1$ 的贡献为 $-\sum\limits_{i=l}^{r-1}\operatorname{dep}(\operatorname{lca}(i,r))$；
这个东西是经典问题，可以离线扫描线处理，所以莫队二次离线即可。
修改次数 $O(n)$，询问次数 $O(n\sqrt m)$。
这个问题的修改为从 $i$ 到根的边权值 $+1$，查询从 $i$ 到根的边权和，树分块即可。
[Ynoi2009] rla1rmdq
题意
给定一棵有根树，边有边权，$\operatorname {dep}(i)$ 为 $i$ 到根的边权和。
给定一个序列 $a$，要求支持两种操作：
- 对于 $l\le i\le r$，$a_i\larr\operatorname {fa}(a_i)$；
- 求 $\min\limits_{i=l}^r\operatorname{dep}(i)$。
不强制在线
题解
序列分块。
先考虑整块处理，注意到边权非负，一个点如果曾经存在于这个块中，这个点就不可能对这个块答案产生贡献，对每个块记一个 $\text {vis}$，然后维护一个当前仍有贡献的集合，每次修改枚举整个集合暴力向上跳，跳到 $\text{vis}$ 的点就删掉，对于一个块均摊复杂度就是优秀的 $O(n)$。
整块修改时打 $\text{tag}$，散块处理时把 $\text{tag}$ 下放，直接用重剖求 $\text k$ 级祖先就行，对于一个位置 $O(\log n)$ 次就会跳到根。所以复杂度是对的。散块修改时，更新后的点要判断一下是否应该加入当前仍有贡献的集合。空间复杂度 $O(n)$，时间复杂度 $O(n\sqrt n)$。
[Ynoi2010] Fusion tree
题意
给定一棵树，点有点权，要求支持下列操作：
- 将与 $x$ 距离为 $1$ 的点点权 $+1$；
- 将 $x$ 点权 $-v$；
- 询问与 $x$ 距离为 $1$ 的点点权的异或和。
不强制在线
题解
对于这种题，我们有一个套路是在每个节点处开一个数据结构维护子节点信息，那么这个数据结构需要支持单独修改一个值，给所有值加一，求所有值的异或和三种操作。我们倒着把数按二进制位插入 $\rm{trie}$ 中显然可以做到第一种和第三种操作，考虑第二种操作，从根节点出发，每次交换左右子树，再进入交换后的 $0$ 子树，记得处理进位。还需要记得维护单点的值，这部分随便处理一下即可。
[Ynoi2010] Brodal queue
题意
给定一个序列区间赋值，询问从一个区间内取出两个数相同的方案数。
强制在线
题解
不弱于小 Z 的袜子，分块。
考虑均摊，如果一个修改只增加 $O(1)$ 个颜色段，每增加/删除一个颜色段的复杂度为 $O(\sqrt n)$，复杂度就是正确的。考虑对于一个块，如果只有一种颜色就不用颜色段表示，否则使用颜色段表示。
对于颜色段表示的块，维护两个块间的答案，块内的答案，每种颜色出现次数的前缀和。
对于非颜色段表示的块，贡献随便计算就行了。
[Ynoi2010] y-fast trie
题意
给定一个常数 $C$，需要维护一个集合 $S$，每次操作插入或删除一个元素并输出 $\max\limits_{i,j\in S,i\ne j}\left((i+j)\bmod C\right)$。
强制在线
题解
所有元素 $\bmod C$ 后加入 multiset，维护与它的和最接近 $C$ 的元素，并更新答案，最终答案为维护的答案和最大的两个元素和取 $\max$，注意 std::multiset::count() 的复杂度为 $O(\log n+cnt)$。
[Ynoi2010] Self Adjusting Top Tree
题意
给出 $n$ 条两两没有公共点的线段（不与坐标轴平行），每次询问一个边与坐标轴平行的矩形，求该矩形和所有线段的交的长度和。
不强制在线
题解
贡献具有可减性，将矩形容斥为前缀矩形，然后只考虑斜率为正的线段，线段分为两种，被矩形包含和与矩形一边有交，第一种可以做二维偏序，第二种只考虑与一边交的，与另一边交的反过来再算一遍就行了，由于线段不交，我们可以扫描线，线段与扫描线的交点顺序不会改变，维护就行了。
[Ynoi2010] Worst Case Top Tree
题意
给定序列 $a$ 满足 $a_0=a_{n+1}=+\infin$，对 $1\le x \le n$，称 $\max_{0\le i<x,a_i\ge a_x} i$ 和 $x$ 是相邻的，且 $\min_{x<i\le n+1,a_i>a_x} i$ 和 $x$ 是相邻的；
如果 $x$ 和 $y$ 相邻，则 $y$ 和 $x$ 也相邻；
如果 $0\le b_1,b_2,b_3,b_4,b_5,b_6\le n+1$，且 $b_i$ 和 $b_{i+1}$ 相邻，$b_1$ 和 $b_6$ 相邻，$b_i$ 互不相同，则称集合 ${b_1,b_2,b_3,b_4,b_5,b_6}$ 是一个六元环（即判断两个六元环是否相同时，不考虑 $b_i$ 的顺序）。
共有 $m$ 次修改操作，每次修改操作给出 $x,y$，将 $a_x$ 改为 $a_x+y$；
每次修改后输出六元环个数。
不强制在线
题解
容易发现求的是笛卡尔树上大小为 $4$ 的连通块数量，但不能包含根节点，使用 $\text{DP}$ 求解，修改操作就是上旋一个节点，用 $\text{LCT}$ 维护链，把一个点旋到链顶只会发生 $O(1)$ 次父子关系的改变，$\text{DP}$ 数组的改变次数也为常数次。
[Ynoi2011] 初始化
题意
给定一个长为 $n$ 的序列 $A$，支持以下操作：
- 给定 $a,b,v$，对所有满足 $k\equiv a\pmod b$ 的 $k$，$A_k=A_k+v$；
- 区间求和。
不强制在线
题解
显然，当 $b\ge \sqrt n$ 时，暴力修改每个点的复杂度正确，使用 $O(1)$ 修改，$O(\sqrt n)$ 查询的分块维护区间和；对于小于 $\sqrt n$ 的 $b$ 我们考虑对于每一个 $b$ 开一个关于 $a$ 的前缀和记录答案，修改时遍历从 $a$ 开始的前缀和数组并对每一个元素进行修改，复杂度 $O(\sqrt n)$，查询时遍历每一个 $b$，$O(1)$ 计算答案。
[Ynoi2011] 遥远的过去
题意
定义 Z 语言：
- 字符集非常大，甚至可能有 $2147483648(2 ^ {31})$ 种字符；
- 每个单词由一系列两两不同的字符组成；
- 字符既能比较相同和不同，也能比较大小，因此之后我们用数字来表示 Z 语言中稀奇古怪的字符；
- 两个看起来完全不同的单词也可能是同一个单词，因为：只要两个单词中第 K 大的字符所在的位置相同，那么其实就是本质上相同的单词。例如 $\begin{Bmatrix}1, 2, 3, 4, 5\end{Bmatrix}$ 与 $\begin{Bmatrix}2, 3, 23, 233, 23333\end{Bmatrix}$ 是相同的。（所以你可以用 Z 语言很方便地加密信息！）
给定两个 Z 语言字符串 $A,B$ 每次单点修改 $B$，询问 $B$ 在 $A$ 中的出现次数。
不强制在线
题解
平衡树维护哈希值，随便搞搞就行了，我的哈希值定义为 $\sum\limits_{i=1}^mrank_i\mathrm{base}^{pos_i}$，单哈希会被卡，双哈希能过。
[Ynoi2011] 成都七中
题意
给定一棵 $n$ 个节点的树，每个节点有一种颜色，每次询问给出 $l,r,x$，求只保留编号在 $[l,r]$ 中的节点时，$x$ 所在连通块的颜色数。
不强制在线
题解
建立点分树，树上任意一个连通块中一定存在一个点满足连通块内元素在其在点分树上的子树内，知道这个性质后，我们便可以把询问放在这个节点上，问题转化为在一棵树上，求从根节点出发，只经过 $[l,r]$ 内的点，能到达的颜色数。我们记录点分树上每一个节点到每一个祖先路径编号的最大最小值 $L,R$ 显然只有 $l\le L\le R\le r$ 才会对答案产生贡献。一个熟练的 oier 会发现这是一道二维偏序水题，先对节点信息和询问信息的 $r$ 排序，在用树状数组维护每种颜色 $l$ 的最大值即可。
[Ynoi2011] 竞赛实验班
题意
维护一个数组 $A$：
- 在数组末尾插入 $x$；
- 输出 $\sum\limits_{i=l}^rA_i$；
- 将所有数异或上 $x$；
- 将 $A$ 从小到大排序。
不强制在线
题解
显然，任意时刻数组的形态都是一个排好序的数组异或上一个数后面接上一些数。维护一个全局异或值，将新插入的数异或上该值再插入。对于排好序的段，使用 $\rm{trie}$ 维护；对于未排序段，拆位计算贡献。每次排序操作，将原未排序段插入 $\rm{trie}$ 中，根据全局异或值维护 $\rm{trie}$ 翻转标记。
[Ynoi2011] WBLT
题意
给定一个长为 $n$ 的序列 $a$，每次询问一个区间 $[l,r]$ 和一个数字 $b$，求最大的 $x$ 使得存在 $a$，满足 $a,a+b,a+2b,\cdots,a+(x-1)b$ 均出现在区间内。
题解
莫队。对于 $b\ge 64$ 的情况，我们开一个 bitset 存每个数是否出现，把每 $b$ 位提取出来与一下，复杂度 $n\sqrt m+\frac{mn}{64}$，对于 $b<64$ 的情况，我们开 $b$ 个 bitset 存每一种 $a$，对每个求一遍 $\operatorname{mex}$ 取 $\max$。
[Ynoi2012] WC2016充满了失望
题意
在平面直角坐标系中，
给 $n$ 个点，这 $n$ 个点是可达的，如果点 $A,B$ 可达则线段 $AB$ 上的点均可达。
给 $m$ 个圆，问有哪些圆满足圆内任意点都是可达的。
不强制在线
题解
问的其实是圆是否完全在凸包内，考虑把圆按照半径排序，我们对半径扫描线，维护收缩了 $R$ 的凸包，只需要查询圆心是否在凸包内，二分即可。
现在的问题是如何维护凸包，考虑一条线被旁边的两条线挤掉的时间，实际上就是与两边线夹角的角平分线交点到该线的距离，用堆维护每条线被挤掉的时间，当一条线被挤掉时，重新计算两边的线被挤掉的时间，对于凸包的维护，我们是要一个支持删除和二分的数据结构，平衡树和并查集都可以。
[Ynoi2012] 惊惶的 SCOI2016
题意
给定一棵 $n$ 个点的树，每个点有颜色，$m$ 次修改单点的颜色，每次修改后输出所有有向简单路径的颜色数量的和。
不强制在线
题解
考虑单独统计每种颜色的贡献，对于每种颜色，我们认为这种颜色为白色，其他颜色为黑色，经过它的路径数量为 $n^2-\sum\text{黑色连通块大小}^2$，用 $\text{Qtree6}$ 的方法维护即可。
[Ynoi2012] NOIP2016 人生巅峰
题意
给定一个长为 $n$ 的序列和一个常数 $v$，有两种操作：
- 对于区间 $l,r$ 内的所有数，变为 $a_i^3\bmod v$；
- 询问区间 $l,r$ 内能否选出两个下标的不交非空集合使得两个集合贡献相等，一个元素对集合的贡献为 $a_i+1$。
不强制在线
题解
因为 $2^{14}-1>14000$，根据抽屉原理，如果询问区间大于 $13$ 则一定有解，我们只考虑询问区间小于等于 $13$ 的的询问。
对于修改，树状数组维护每个数立方了几次，询问时算出区间内数的实际值即可。
用 bitset 优化背包即可通过小于等于 $13$ 的询问。时间复杂度 $O(m\frac{13^2v}{w})$。
[Ynoi2013] 无力回天 NOI2017
题意
维护一个序列 $a$，支持两种操作：
- 对于区间 $[l,r]$ 内的每一个数 $a_i$，$a_i=a_i\operatorname{xor} v$；
- 求在区间 $[l,r]$ 内任选任意个（包括 $0$ 个）数 $\operatorname{xor}$ 起来，这个值与 $v$ 的最大异或和。
不强制在线
题解
用树状数组维护区间异或单点查询，再用线段树维护差分数组的区间线性基，查询时取出 $[l+1,r]$ 的线性基，插入 $a_l$ 后得到的线性基与原数组中 $[l,r]$ 的线性基等价，直接查询即可。
[Ynoi2013] 文化课
题意
维护一个只有 $+,\times$ 和数的表达式，支持：
- 对数区间赋值；
- 对符号区间赋值；
- 区间求值。
不强制在线
题解
考虑使用线段树维护。
不考虑第一个操作的维护是简单的，只需要维护第一个操作。
$x$ 满足 $\sum x_i=n$ 则 $x_i$ 只有 $\sqrt n$ 种取值，所以连乘段只有 $\sqrt n$ 种长度，对于线段树一个节点，维护所有连乘段长度即出现次数，区间赋值时光速幂计算（光速幂块长的平方应等于区间总长而不是 $n$）。
复杂度为 $T(n)=2T(\frac n2)+O(\sqrt n)=O(\sqrt n)$， 总复杂度 $O(m\sqrt n)$。
[Ynoi2013] 对数据结构的爱
题意
给定一个序列 $a$，每次查询 Sum(a,l,r,p) 的运行结果。
不强制在线
题解
一个数通过一个区间的时候，$-p$ 的次数随这个数的增大单调递增，线段树双指针合并一下就好了，查询的时候二分即可。
[Ynoi2013] 大学
题意
维护一个序列 $a$，支持两种操作：
- 把区间 $[l,r]$ 内的每一个 $x$ 的倍数除以 $x$；
- 求区间 $[l,r]$ 的和。
强制在线
题解
对于每一个数开一个 std::vector 存储所有倍数的位置，用并查集维护 $\rm{nxt}$ 数组，树状数组维护区间和，每次修改都暴力在树状数组里修改，注意判掉 $x=1$ 的情况。
[Ynoi2013] D2T2
题意
给定一个序列，每次查询将值在 $[L,R]$ 内的值保留不变，其他值变成 $0$，求区间 $[l,r]$ 内的最大子段和，询问独立。
不强制在线
题解
对于一个长为 $n$ 的序列，本质不同的值域区间数量为 $O(n^2)$，考虑分治，我们显然有一种 $T(n)=2T(\frac{n}{2})+O(n^2)=O(n^2)$ 的分治方法求出在所有值域限制下的信息（指最大前缀和、最大后缀和、区间和、最大子段和）。对序列分块，每一块都这么处理，并统计对询问的贡献，实现上注意要使用双指针而不是二分。
[Ynoi2013] Ynoi
题意
给定一个序列，支持区间异或，区间排序，区间求异或和。
题解
平衡树套 $\text{trie}$，节省空间，使用压缩 $\text{trie}$。
平衡树每个节点表示一个连续段 $([l,r],v)$，表示排好序的 $l,r$，异或上了 $v$。
区间操作就分裂出这个区间，区间排序就把所有 $\text{trie}$ 合并到一起即可。
[Ynoi2014] 等这场战争结束之后
题意
给你一个图，每个点有点权，最开始没有边。
有一些操作：
添加一条 $x$ 与 $y$ 之间的双向边。
回到第 $x$ 次操作后的状态（注意这里的 $x$ 可以是 $0$，即回到初始状态）。
查询 $x$ 所在联通块能到的点中点权第 $y$ 小的值。
不强制在线
题解
我们考虑建出操作树，先进行一次 $\text{dfs}$，将加边操作判断是否合法（是否已连通），处理出操作树上每个加边操作并查集的根，询问操作并查集的根。
将权值离散化，使得每个权值唯一对应一个点，对值域分块。
对于每个值域块进行一次 $\text{dfs}$，得出每个询问的答案在哪一个值域块内。
对操作树分块，这里分块的要求是选出 $O(\frac{m}{B})$ 个点使得树上任意一个点存在一个不超过 $O(B)$ 级祖先为关键点，$B$ 取 $\sqrt{m}$。
我们称一个点所属的块的根为离它最近的为关键点的祖先（包括自己），有同一个所属的块的根的节点属于同一块。
对于每一个块，我们可以 $O(m)$ 处理出操作到这个块根时，每个点所属的并查集的根。块内每个询问的状态是从根处状态合并 $O(B)$ 次连通块形成的，我们把这 $O(B)$ 次合并连通块拿出来，$\text{BFS}$ 一遍就可以知道哪些并查集的根与询问节点属于同一连通块，枚举答案所在值域块内点，得到答案，我们就完成了一个时间 $O(n\sqrt{n})$，空间 $O(n)$ 的算法，$n,m$ 同阶。
[Ynoi2014] 人人本着正义之名
题意
给你一个 $\text{01}$ 序列，要求支持以下操作：
- 区间赋值；
- 对于区间内每一个数与/或上其左边/右边的数；
- 查询区间和。
强制在线
题解
使用平衡树维护连续段，容易发现第二种操作就是连续段的扩张和收缩。
在维护过程中，我们发现必须要保证连续段极长，所以插入时需要判断一下前驱和后继是否同色。
注意到第二种操作会产生长度为零的连续段。对于每个连续段只会被删除一次，连续段共 $O(n+m)$ 个，对于每个，直接 $O(\log n)$ 删除，并判断左右是否应合并，这样总复杂度就是 $O((n+m)\log n)$ 的。然后就是实现上有很多细节，慢慢实现就好了。
[Ynoi2015] 我回来了
题意
亵渎描述为：等概率随机在 $[l,r]$ 中选出一个整数作为伤害值 $d$，对所有随从造成 $d$ 点伤害，如果有随从死亡，则再次施放该法术，但伤害值不重新随机；如果没有随从死亡，则停止释放。
支持两种操作：
- 在场面上加入一个血量为 $h$ 的随从，这里随从的血量都不能超过 $n$；
- 给定 $l,r$，询问亵渎期望触发多少次，答案乘 $r-l+1$ 输出。
不强制在线
题解
注意到期望乘 $r-l+1$ 其实就是 $d$ 取 $[l,r]$ 内每一个整数时释放次数的和，当 $d$ 固定时，求的就是最小的 $i$ 使得血量为 $[(i-1)d+1,id]$ 的随从均不存在。
求出每个血量的随从第一次被加入的时间，上面的区间只有 $O(n\log n)$ 种（调和级数），所以我们可以用 $O(n\log n)-O(1)$ 的 ST 表求出每个区间第一次有随从的时间，再对相同长度的区间求前缀 $\max$，在这个值后，这段区间才会产生贡献，树状数组维护即可。
[Ynoi2015] 纵使日薄西山
题意
给定一个序列，支持单点修改，每次修改后询问进行几次下面的操作会使得序列全小于等于零，询问独立。
选出最大值位置 $i$，把 $a_{i-1},a_i,a_{i+1}$ 全部减一。
题解
对于一段单调区间，显然答案是第一大+第三大+第五大……，用 set 维护极值，两个树状数组维护奇数位和偶数位的区间和，注意边界。
[Ynoi2015] 即便看不到未来
题意
给定一个序列，每次查询一段区间内长度为 $1,2,\dots,10$ 的极长值域连续段分别有多少个，极长值域连续段 $[l,r]$ 满足条件 $[l,r]$ 内的所有数都出现在这个区间内，$l-1,r+1$ 没有出现在这个区间内，它的长度是 $r-l+1$。
不强制在线
题解
考虑扫描线，对于右端点相同的询问，使用数据结构维护不同左端点处的答案。每加入一个数，只用考虑这个值前后各 $10$ 个值，把这些值最靠右的出现位置记下来，从右往左扫过去，更新答案即可。
[Ynoi2015] 此时此刻的光辉
题意
给定一个序列，每次查询区间乘积的约数个数 $\bmod 19260817$ 的结果。
不强制在线
题解
考虑莫队，这题显然有一个 $O(n\sqrt m\log a)$ 的暴力，我们考虑将小于 $1000$ 的质数出现次数的前缀和预处理出来，这样每个数只剩最多两个质因子了，莫队时候维护即可。
[Ynoi2015] 盼君勿忘
题意
给定一个序列，每次查询区间 $[l,r]$ 内所有子序列分别去重后的和 $\bmod p$，注意：每次询问 $p$ 不同。
不强制在线
题解
在区间 $[l,r]$ 内，$k$ 出现了 $cnt_k$ 次，则它对答案的贡献为 $k(2^{r-l+1}-2^{r-l+1-cnt_k})$，不同的出现次数只有 $O(\sqrt n)$ 种，所以直接莫队，暴力光速幂计算答案即可。
[Ynoi2015] 世上最幸福的女孩
题意
给定一个序列，支持全局加，区间查询最大子段和。
不强制在线
题解
建立线段树，线段树每个节点维护三个上凸壳，横坐标为长度，纵坐标为和，分别维护最大子段和，最大前缀和，最大后缀和，合并的时候闵可夫斯基和左子树的最大后缀和和右子树的最大前缀和。
查询的时候直接在线段树上二分，这样复杂度为 $O(m\log^2n)$，按照全局加的大小排序，此时凸包上决策点单调，挪指针就行了，均摊复杂度为 $O(n\log n+m\log n)$。
[Ynoi2016] 掉进兔子洞
题意
给定一个序列，每次询问三个区间，把重复的数一个一个地删除，求剩余数的个数。
不强制在线
题解
直接莫队，离散化之后上 bitset，答案就是三个区间 bitset 的与和的 $1$ 的数量。
[Ynoi2016] 这是我自己的发明
题意
给定一棵树，有点权，支持两种操作：
- 换根；
- 从 $x$ 的子树中选每一个点，从 $y$ 的子树中选每一个点，求点权相等的情况数。
不强制在线
题解
倍长 $\text{dfn}$，换根是假的，每个子树对应一个区间，问题转化为从 $[l_1,r_1]$ 中选每一个数，从 $[l_2,r_2]$ 中选每一个数，数相等的情况数，设答案为 $f([l_1,r_1],[l_2,r_2])$，$f([l_1,r_1],[l_2,r_2])=f([1,r_1],[1,r_2])-f([1,l_1-1],[1,r_2])-f([1,r_1],[1,l_2-1])+f([1,l_1-1],[1,l_2-1])$，问题转化为求 $f([1,a],[1,b])$，像莫队一样移动 $a,b$ 两个指针并统计答案即可。
[Ynoi2016] 镜中的昆虫
题意
给定一个序列，要求支持区间染色和区间数颜色。
不强制在线
题解
不考虑修改，区间数颜色可以转化为经典的二维数点问题，把每个位置看做 $(i,pre_i)$ 询问的就是有多少个点在矩形 $l\le x\le r,y<l$ 内。
区间染色的 $pre$ 改变是 $O(n+m)$ 的，所以问题变为单点修改，加一维时间，若删除就加一个点权为 $-1$ 的点，三维数点，$\text{cdq}$ 分治板子。
[Ynoi2016] 炸脖龙 I
题意
给定一个序列，支持两种操作：
- 区间 $[l,r]$ 加 $x$；
- 查询 $a_l^{a_{l+1}^{\dots^{a_{r}}}}\bmod p$。
不强制在线
题解
树状数组维护区间加单点查询，对于询问，用扩展欧拉定理降幂，一个 $\text{dfs}$ 完事，记得筛 $\varphi$。
[Ynoi2017] 由乃的 OJ
题意
给你一个有 $n$ 个点的树，每个点的包括一个位运算 $opt$ 和一个权值 $x$，位运算有三种 &、|、^，分别用 $1,2,3$ 表示。
每次询问包含三个整数 $x,y,z$，初始选定一个数 $v$。然后 $v$ 依次经过从 $x$ 到 $y$ 的所有节点，每经过一个点 $i$，$v$ 就变成 $v\ opt_i\ x_i$，所以他想问你，最后到 $y$ 时，希望得到的值尽可能大，求最大值。给定的初始值 $v$ 必须是在 $[0,z]$ 之间。
每次修改包含三个整数 $x,y,z$，意思是把 $x$ 点的操作修改为 $y$，数值改为 $z$。
不强制在线
题解
考虑序列上如何用线段树维护，即如何合并两个区间，记录全 $1$ 的数和全 $0$ 的数通过区间后的答案，对于经过整个区间后变成 $1$ 的位，只有两种可能，在经过左区间后是 $1$，经过右区间后仍是 $1$；经过左区间是 $0$，经过右区间后变为 $1$，即 $ans_0=(l_0 \operatorname{bitand} r_1)\operatorname{bitor}(\operatorname{compl} l_0\operatorname{bitand}r_0),ans_1=(l_1 \operatorname{bitand} r_1)\operatorname{bitor}(\operatorname{compl} l_1\operatorname{bitand}r_0)$。直接上树剖加线段树，LCT，全局平衡二叉树都行。
[Ynoi2017] 由乃的玉米田
题意
给你一个序列 $a$，长度为 $n$，有 $m$ 次操作，每次询问一个区间是否可以选出两个数它们的差为 $x$，或者询问一个区间是否可以选出两个数它们的和为 $x$，或者询问一个区间是否可以选出两个数它们的乘积为 $x$，或者询问一个区间是否可以选出两个数它们的商为 $x$（没有余数），这四个操作分别为操作 $1,2,3,4$。
不强制在线
题解
对于前两个，直接莫队加 bitset。对于第三个，莫队加 bitset 暴力枚举因数。对于第四个，如果 $x\ge \sqrt n$，莫队加 bitset 暴力枚举倍数；否则对于每一个 $x$，扫一遍序列处理。
[Ynoi2017] 由乃打扑克
题意
给定一个序列，操作：
- 区间 $[l,r]$ 加上 $k$；
- 求区间第 $k$ 小值。
不强制在线
题解
分块，块内存排序数组，然后二分，再卡卡常。
当然，多序列二分可以用分散层叠优化。
[Ynoi2018] 五彩斑斓的世界
题意
给定一个序列 $a$，操作：
- 把区间 $[l,r]$ 中大于 $x$ 的数减去 $x$；
- 查询区间 $[l,r]$ 中 $x$ 的出现次数。
不强制在线
题解
先分块，逐块处理，对于每块我们用并查集维护相同的值，设置区间减的 $\text{tag}$，并维护最大值 $k$。若 $2x\ge k$，把大于 $x$ 的数减去 $x$；否则，把小于等于 $x$ 的数加上 $x$，并让 $\text{tag}=\text{tag}+x$。
[Ynoi2018] 末日时在做什么？有没有空？可以来拯救吗？
题意
给定一个序列，支持区间加，查询区间最大子段和。
不强制在线
题解
序列分块，逐块处理，每一块内分为全局修改，区间修改，全局查询，区间查询，先不考虑区间修改，这道题就是 [Ynoi2015] 世上最幸福的女孩 只要把排序变成基排即可。
按区间修改把询问分段，每段按照 [Ynoi2015] 世上最幸福的女孩 做，段的总数为 $O(m)$，每次把根节点的指针归位，这部分总复杂度为 $O(m\sqrt n)$，区间查询时直接二分，区间查询的次数为 $O(m)$，这部分复杂度为 $O(m\log^2n)$，区间修改时就像普通的线段树一样修改，pushup 部分总复杂度为 $O(\sqrt n)$，所以这部分总复杂度为 $O(m\sqrt n)$。
[Ynoi2018] 未来日记
题意
给定一个序列 $a$，操作：
- 把区间 $[l,r]$ 中所有 $x$ 变成 $y$；
- 查询区间 $[l,r]$ 中的 $k$ 小值。
不强制在线
题解
序列分块，值域分块，并查集维护相同的值，值域分块 $O(\sqrt n)$ 查询 $k$ 小值，维护每一种数在每一块内的出现次数和前缀和，维护每一块数在每一块内的出现次数的前缀和。
[Ynoi2018] 天降之物
题意
给定一个序列 $a$，操作：
- 把所有 $x$ 变成 $y$；
- 找出一个位置 $i$ 满足 $a_i=x$，找出一个位置 $j$ 满足 $a_j=y$，使得 $\mid i-j\mid$ 最小，并输出 $\mid i-j\mid$。
强制在线
题解
使用 vector 存储每种元素的出现位置。根号分治，出现次数大于 $\sqrt n$ 的元素不超过 $\sqrt n$ 个，对这些元素预处理出它们和所有元素的答案，并不存储预处理过的位置，新增位置若不足 $\sqrt n$ 的也存到 vector 里，否则再次预处理，每次询问扫一遍 vector 即可。
[Ynoi2018] GOSICK
题意
给定一个序列 $a$，每次询问给一个区间 $[l,r]$。查询 $l \leq i,j\leq r$，且 $a_i$ 是 $a_j$ 倍数的二元组 $(i,j)$ 的个数。
不强制在线
题解
莫队二次离线，显然只有在前缀 $[1,i]$ 中有多少个数是 $a_j$ 的倍数一种离线下来的询问不能 $O(\sqrt n)$ 插入 $O(1)$ 查询。考虑根号分治，对于大于 $\sqrt{\max\begin{Bmatrix}a\end{Bmatrix}}$ 的显然可以暴力向倍数的位置贡献，复杂度正确；对于小于 $\sqrt{\max\begin{Bmatrix}a\end{Bmatrix}}$ 的，我们的询问是 $O(m)$ 个形如在前缀 $[1,i]$ 中有多少个数是 $[l,r]$ 内数的倍数，这部分的答案是 $\sum\limits_{v=1}^{\sqrt{max{a}}}\left(\sum\limits_{j=1}^i[a_j=v]\right)\left(\sum\limits_{x=l}^r[a_x\equiv0\pmod v]\right)$。
[Ynoi2018] 駄作
题意
给定一棵树，每次询问两个邻域，求从两个邻域各选一个点，两点间距离的和。
不强制在线
题解
一个邻域可以被拆分成不同块内的 $O(B)$ 个邻域，其中只有 $O(1)$ 个邻域的中心不是界点。
先对每个块单独处理，只考虑同一块内的两个邻域的贡献，分两种情况。
- 两个邻域的中心有至少一个不是界点，这种情况总共只有 $O(m)$ 次。我们知道 $d(a,b)=d(rt,a)+d(rt,b)-2d(rt,\operatorname{lca}(a,b))$，我们只要知道 $\sum d(rt,\operatorname{lca}(a,b))$ 就可以了。对一个邻域内的点到根的路径全部加一，求另一个邻域内的每个点到根的路径的权值和就是我们要求得值，总时间复杂度 $O(mB)$。
- 两个邻域的中心都是界点，中心只有三种情况，半径只有 $O(B^2)$ 种情况，所以总情况数只有 $O(B^2)$ 种，预处理出来就行了，预处理的方法是枚举第一个邻域的半径，然后用上面的方法就可以求出第二个邻域所有半径下的答案，总复杂度 $O(\frac {n}{B}B^2)=O(nB)$。
在考虑不同块之间的贡献，对于两个不相交的邻域，有一个求出答案的方法，找到一个点使得从两个邻域中各选一个点路径必定经过这个点。只要求出每个邻域所有点到这个点的距离和点的个数，称为 $d_i,c_i$，则答案为 $d_0c_1+d_1c_0$。对每个询问每个块求出邻域在这个块内点的个数和到两个界点的距离和，在收缩树上按照这个式子 $\text{dp}$ 一下子就完事了。
时间复杂度 $O((n+m)\sqrt n)$，空间复杂度 $O(n+m)$。
[Ynoi2019] 魔法少女网站
题意
给定一个序列，操作：
- 将 $x$ 位置的值修改为 $y$；
- 查询区间 $[l,r]$ 中有多少子区间的最大值小于等于 $x$。
不强制在线
题解
操作分块，对于同一块内的询问，按 $x$ 排序，被修改的位置单独处理，每次先修改，再遍历所有被修改的位置，计算答案，撤销影响。问题转化为有一个 $01$ 序列，两种操作，$O(1)$ 把 $0$ 变成 $1$，$O(\sqrt n)$ 查询在一个区间内，设极长连续的 $1$ 长度为 $i$，求 $\sum \frac{i(i+1)}{2}$。序列分块，维护极长连续段的头和尾，用链表维护相同的值的位置，对于每个询问，先加入所有小于 $x$ 的值，再处理被修改的位置 ，在一整块的询问处理完毕后，将修改的影响加到原序列上。
强制在线做法：序列分块，每块内不同的答案只有 $O(\sqrt n)$ 种，查询是在所有整块内二分，修改是单点修改，分散层叠即可。
[Ynoi2019] Happy Sugar Life
题意
给定一个排列，每次询问给一个区间和一个值域区间，求在范围内的顺序对数。
不强制在线
题解
分块，散块对整块，散块对散块，散块内部三部分的贡献变为 $O(m\sqrt n)$ 次查询 $[l,r]$ 内值在 $[x,y]$ 内的数的个数，扫描线 + 值域分块处理。
整块内部只有 $O(B^2)$ 种本质不同的值域区间，每个块 $O(B^2)$ 递推一下所有的答案就行了。
整块对整块，考虑值域区间变成值域上的前缀时的答案计算，可以把所有数从小到大加入，记录 $f_{i,j}$ 表示 $i\sim j-1$ 块对第 $j$ 块的贡献，加入第 $p$ 个块的数只影响 $f_{x,p}$，暴力修改即可。我们用 $[1,y]$ 时的答案减去 $[1,x-1]$ 时的答案，现在多出的部分是前面块 $[1,x-1]$ 部分乘上后面块的 $[x,y]$ 部分，直接值域分块计算就可以了。
[Ynoi2019] 美好的每一天~ 不连续的存在
题意
给定一个数组 $A$，以及一棵 $n$ 个节点的树，每个点有一个颜色，颜色为 $1$ 到 $x$ 的整数。每次查询树上只保留 $[l,r]$ 内的所有节点，设一个极大连通块中出现奇数次数的颜色个数为 $t$，则其对答案的贡献为 $A_t$，即答案是所有连通块贡献的和，询问间互相独立。
不强制在线
题解
注：这里回滚莫队的写法为同一块内暴力，右端点在同一块内的询问，按左端点排序。
考虑如何合并连通块，我使用的方法是压位 $\rm{trie}$（这个东西到底叫什么我也不太清楚）合并，显然复杂度是均摊的。考虑回滚莫队，如果不算回滚部分的复杂度，复杂度显然正确，均摊复杂度为 $O(n\log n)$，也就是说，我们必须让一个块内插入所有节点时总复杂度在 $O(\frac{n\log n}{\sqrt m})$ 内。考虑先模拟一遍最劣情况下的回滚，即左侧所有点都已插入，这时在插入这个点的时间消耗就是最劣情况，如果消耗大于 $O(\frac{n\log n}{\sqrt m})$，则将这个点作为新块的左端点，等价于对一个长为 $O(n\log n)$ 的序列分块。但单个点插入的复杂度可能远超 $O(\frac{n\log n}{\sqrt m})$，我们发现，这样的点一定是左端点，而在处理右端点在这个块内的询问的时候，所有询问必然包含这个点，我们直接在处理询问前将其设为存在的节点，这样插入这个点的复杂度便是 $O(1)$。
[Ynoi2077] hlcpq
题意
给定 $n$ 条纵坐标不同的水平线段和 $n$ 条横坐标不同的竖直线段，两个线段有交则连一条边，求哪些线段是割点。
题解
很容易发现这张图可以主席树优化建图，但优化建图会带来虚点，割点就会改变，所以不能建出虚点。
为便于理解，放一个求割点的代码。
void tarjan(int x){
int c=0;
low[x]=dfn[x]=++cnt;
for(int u:g[x])
if(!dfn[u]){
tarjan(u),++c;
if(dfn[x]==low[u]) f[x]=1;
low[x]=min(low[x],low[u]);
}else low[x]=min(low[x],dfn[u]);
if(x==startpoint) f[x]=c>1;
}
我们的主席树维护区间 $\min$，然后每次找到一个没访问过的点，$\text{tarjan}$ 下去就行了。